近直、自動微分で政策課題を解決してみよう、という投稿を考えているのですが、自動微分についてのネット上の情報が極めて少なく、ほぼ、初学者向けの情報は皆無と言えるので、せっかくなので事前のエントリー記事を書きます。
大学の数学では、偏微分をならった。
高校生の数学で習って大学入試とかで使う微分と、偏微分の違いは何かと言うと
微分は
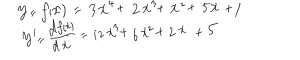
という感じで、ある関数の変数の一つに注目して、上記の関数だとxに注目して微分します
余談だけど、僕は高校の時は微分より積分の方が苦手だったけど、パソコンで計算すると積分は、その原理上、数値計算が楽なので、現時点では積分より微分の方がとても難しかったなと感じています。そもそも現時点は微分、積分なんて日常生活では使いません。
さて、微分に対して、偏微分は
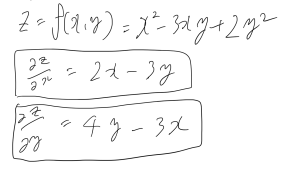
という感じに、2つ以上の変数を含んだ関数について、ある一つの変数について微分することを偏微分と呼びます。
そもそも微分の定義は、

直感的には、関数f(x)の接線の傾きが微分と表現できます。そして、このhという値は十分に小さいのですが、これが問題です。どれくらい小さいかというと、パソコンで具体的に計算する時は、例えば、0.001だったり、0.0000000001とかだったりします。この数字をどうするかで、計算精度が変わるのですが、一応、目安となる法則があるらしいですが、この塩梅の理屈が僕には正直わかりません。
次に最適化について、ニュートン法を復習?、します。ニュートン法は、大学でも数学とか物理では勉強せず、プログラミングの授業で、熱力学のシュミレーションで習った気がします。最適化ってなにかというと、関数f(x)=0 の時のxの値を見つけ出すという行為です。なんで、関数f(x)=0 の時のxの値を探すかというと、それが一番ちょうどいい!とされる値だからです。この辺りは、また次回以降、実例で解説します。
ニュートン法の具体的な実行手順は、

今回はここまで。次回は微分の復習、合成関数の微分と一緒に、ニュートン法とは別のやり方の自動微分の基礎について解説していきます。







最近のコメント