今回のブログは、自分で計算するのではなく、Pythonというプログラムを使って、パソコンで微分をしてみよう、という内容です。
いきなり、自動微分をプログラムするのは難しいので、まずは数値微分のプログラムの紹介です。ちなみに、僕はプログラミングはfortran77しかやったことないです。ただ、自宅のパソコンにfortranのコンパイラがないし、ネットで探すのも面倒くさいので、これを機に、Pythonで微分をやってみましょう。
classで任意の、例えばlogとか好きな関数を定義して、求めたい関数になるように組み合わせれば、その関数の導関数値を求めることができます。高校生の授業や大学受験で苦しんだ微分も、プログラミングを使えば簡単に解けます。ただ、パソコンではlim h→0というように無限大に小さいという概念は、現実的にはh=0.0001などと定義してあげる必要があり、誤差の原因になることと、数値微分はあくまで導関数値という数字を求めることであり、導関数を求めることができない点に注意が必要です。


ゼロから作るdeep learning 3 から、プログラムは持ってきました。とてもおもしろいので、出版したら買います。https://www.dropbox.com/sh/l9cw1jmozqel6ps/AAC0MVzIwjH9S6ge4AN6f0n-a?dl=0&preview=stage1.pdf#







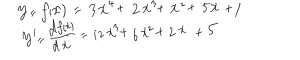
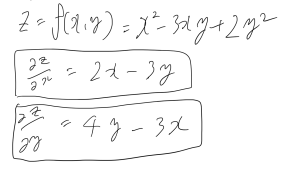


最近のコメント