名古屋民主のくにまさ直記です。議長のお許しがありましたので、通告に従い順次質問致します。4年ぶりの質問、長くもあり、今思えば短くもあり、様々な思いが詰め込まれた4年間、議員を経験した後、ひとりの市民として市政を注視してまいりました。
その中で私がもっとも驚きを感じたのは、今から述べる東区役所の改築に関する経緯と今後の方向性であります。いち東区民としての立場から、区民の声を代弁し、質問をさせて頂きます。
さて、東区役所は、昭和45年10月に竣工し、築53年で老朽化が著しく早急に改築が必要です。そうした行政課題を認識しつつ、いち区民の立場においては、東区役所の改築はおそらく現地改築の方向性で進んでいるのだろう、と思い込んでおりました。
しかし、急遽、3月10日の中日新聞朝刊をはじめとして、東区役所の移転改築の方針を知ります。この話は、元議員として市政を注視していた私にとっても寝耳に水の出来事であり、区民の皆様も困惑しております。そもそも移転について知らない人も多く、様々な過去の経緯から現・東区役所での現地改築をするのだろうと今でも認識している方もみえます。なぜ、現地改築では駄目なのか、どうして愛知大学車道キャンパスへの移転改築の方針を急遽示したのか、行政から区民への丁寧な説明がないまま新聞報道と噂話のみが残され、議会だけで粛々淡々と物事が先行していく事態に対して、区民不在なのではないかと危惧しております。
現東区役所は、東消防署と警察署にほぼ隣接しており、災害対策の拠点として申し分ない位置関係にあり、しかも、50年以上にわたり区民に親しまれてきた場所であるからにして、本来は現地改築がベストであるというご意見もあり、現在の方針に対して調査や情報整理を本当に尽くしたのかどうか不安を抱いている区民もいます。
その不安の声がある以上、なぜ、車道キャンパスへの移転改築を検討しているのかという区民への説明が必要です。
令和5年度事業として、東区役所の整備に向けた建物調査が認められた後、当局が東区民への説明と理解を求める働きかけをどの程度実施しているのか確認したところ、5月中旬の段階で説明を行ったのは、たった2人にしか行われていない状況でした。これは流石に、区民不在の東区役所整備だとの指摘が出ても仕方のないことではないでしょうか。
本市においては他の用途の建物から区役所に転用した事例がなく、大学校舎は飽くまで校舎として建てたものであり、区役所の業務に供するには利便性や機能性が劣るのではないかと心配しており、実際に6月2日に各学区から東区役所に提出された区政要望には新築での建設を要望する意見もあったと確認しております。
私は区民の賛否両論の意見があることを認識し、まずは賛成反対の立場を超えて、現地視察をするべく、愛大車道キャンパスと、さらに参考として本年1月4日にオープンした中村区役所を視察しました。車道キャンパスは13階建の高層階で駐車場も多くスケールの大きさを感じる一方、新中村区役所は庁舎内部だけでなく出入口にエレベーターを設置することで車椅子(いす)利用者を含めて区民が目的のフロアに直結してアクセスできるなど配慮が十分に行われていたり、ホールの天井の高さを式典行事だけでなくレクバレーやインディアカなどができる高さで設計されており、多くの目的に対応する区役所ならでは構造設計であると感じました。
愛大車道キャンパスに関して気になったのが現在築19年であり、本年度の調査の結果次第では、このまま整備にかかる基本構想や基本計画の策定(さくてい)、設計などが順調に進んだとしても改修工事を含めると、実際には早くて築30年弱の構造物を次の東区役所として使うことになります。
車道駅徒歩2分の立地は桜通線沿線住民や名古屋駅からの来訪者には便利であることは間違いありませんが、東区を通る桜通線は高岳駅のみであり利用者の大多数を占める東区在住者にとっては大きく利便性が向上しているとは言いがたく、各種手続きや災害時等における連携に必要な東消防署及び警察署までの距離も今より500メートル離れることになります。
区役所は地域行政の要です。災害対策の拠点となることから、来るべき東南海(とうなんかい)地震に備えて堅牢な耐震構造が求められ、今後、未知の新興(しんこう)感染症に備える観点からも、これに対応した空調設備やパーティションの工夫・配慮を備えるべきです。
このような状況の中、他の区役所が今までに1つの例外もなく全て新築であることを踏まえ、本年度の建物調査を進めるにあたって、こうした区民の不安・不満の声に寄り添い、できるだけ多くの区民に最大限満足していただける区民による区民のための区役所を改築して頂きたいです。
そこで、スポーツ市民局長に伺います。
東区役所の整備は、既存建物の用途転用ではなく新築での整備を望む区民の声も聞いておりますが、用途転用での整備について、区役所の利便性や機能性を確保した建物とすることができるのか考えをお聞かせください。
また、車道キャンパスでの整備を行う場合、竣工までどのようなスケジュール感で
進められるのかお答えください。
あわせて基本構想に区民の意見を盛り込む必要があると考えますが、その予定はあるのでしょうか。その場合、早急に区民に東区役所の整備について説明する機会を設けるためにも、住民説明会やアンケート調査などを実施する計画はあるのでしょうか。
以上、お尋ね致します。
答 弁
議員ご指摘のとおり、区役所は多くの区民の皆さまにご利用いただく施設であり、日常業務に加え、災害時には地域防災活動拠点としての機能も備えている施設である。区役所を新築する場合でも、既存建物の用途転用の場合であっても、区民の皆様にとって使い勝手がよく、防災活動に支障のない耐震性等を備えた施設とすることが重要であると認識している。
今年度実施している建物調査の中で、利便性等も踏まえながら、区役所としての機能を十分に確保できるかどうかについてしっかりと検討を進めてまいりたい。
また、区役所の整備にかかる標準的なスケジュールとしては、基本構想の策定、基本計画の策定にそれぞれ1年を要するほか、設計に2年、工事等に3年程度要するものであるが、仮に車道キャンパスでの庁舎整備を実施することになった場合のスケジュールについては、建物調査の結果や大学との協議等を踏まえて、今後具体的に決まっていくものと考えている。
最後に、区役所整備については、区民の皆さまにとって大変関心のある事柄だと認識しており、地域の代表者の皆さまにはご説明をしながら進めさせていただいているところだが、今後も調査結果で一定の方向性が出る年内のタイミングをはじめ、節目節目において、区役所とも連携しながら、学区などからの要望に応じて直接に説明に出向くなど、区民の皆さまに丁寧にご説明をさせていただくとともに、ご意見・ご要望を踏まえながら進めてまいりたい。
要望
今年度実施している建物調査は、本市として1度の前例もない、民間施設の用途転用を行い、改修工事を行うことで東区役所として移転を行う調査であります。
しかし、それに対し区民の反応は、移転改築の方針に対して、まして民間施設の用途転用に関しては、知らんかった、それで本当に大丈夫なのか?という反応であります。
区役所は1度整備すれば当然、長く使うものですから、これから生まれてくる子どもたちも含めて、区民不在ではなく、誰のための、何のための区役所なのかを強く意識して区民と一緒に、一丸となって整備に取り組んでいくことが理想です。
そういう意味で、この質問は東区の公職者としての質問ではあるものの、その大前提として一人の平成生まれの若者として、もっと言えば、私の子どもに至っては令和生まれでありますし、とにかく、若い世代の代表としての立場でも質問しています。新たな東区役所に禍根を残すことなく区民が愛着と誇りをもって長期間活用していただけるような内容で改築整備をしていただくことを強く要望いたします。
まだ調査結果の中間報告もないことから、質問の内容に対する答弁に十分な理解と納得を得ることができませんので、また機会を見て次の議会や、会派先輩議員の協力を得ながら委員会等で引き続き質疑を重ねてまいりたいと存じます。以上で質問を終わります。


トップ ≫ ブログ
» ヘラクレスオオカブトの幼虫の覚書
現在飼育中のカブトムシは
ヘラクレスヘラクレスが幼虫35匹、成虫が雄雌3ペア
リッキーの幼虫が2匹
ヘラクレスヘラクレスが幼虫35匹、成虫が雄雌3ペア
リッキーの幼虫が2匹
» 備忘録 スマートフォンがUSBデバックに反応しないとき
https://sp7pc.com/google/chrome/18567#toc5
usbデバックのパソコンの接続がうまくいかないとき
別のアプリのduetっていうパソコン側のアプリが邪魔をしていた。
アンインストールすると解決。ただし、一度スマフォを再起動する必要があった。
該当端末はoppo2020とranoA
キーボード操作とマウス操作がwindowsで使えてとても便利
usbデバックのパソコンの接続がうまくいかないとき
別のアプリのduetっていうパソコン側のアプリが邪魔をしていた。
アンインストールすると解決。ただし、一度スマフォを再起動する必要があった。
該当端末はoppo2020とranoA
キーボード操作とマウス操作がwindowsで使えてとても便利
» リコール運動の不正署名問題について
リコール運動の不正署名問題では、1000万円を超えるバイト代が支給されたことが判明しています。そのアルバイトに参加した複数人が、「(アルバイトに参加したので)処罰されないだろうか」という不安の声が上がっています。
専門家によれば、「犯罪は成立しているが、逮捕・起訴はされない可能性がある」とのことです。一方、刑事法が専門の加藤克佳教授(名古屋市出身旭丘高校・早稲田法学部卒)は「判例上では、立件に違法性の認識の必要はない」と指摘しています。
確かに、違法駐車で切符を切られた後に、「ここが駐禁とは知らかった!」という理由で違反が無効になることはありません。立件されるされないのどちらであっても、アルバイトに参加した人が違法な犯罪に手を染めたという事実は残ります。
私は、政治活動は大切な暮らしの一部で、老若男女問わずもっと身近であってほしいと願っています。困っている当事者や支援者のひとり一人の声を署名という形で集めて、議会や行政に届けることは政治活動の大きな柱です。それを、こんな稚拙でだらしのない違法行為が行われニュースになれば、政治に詳しくなかったり興味がない人たちは、ただでさえ距離がある政治に対してより一層の嫌悪感をもつはずです。
それが悔しいです。
中日新聞社会面(1,31面)参考
専門家によれば、「犯罪は成立しているが、逮捕・起訴はされない可能性がある」とのことです。一方、刑事法が専門の加藤克佳教授(名古屋市出身旭丘高校・早稲田法学部卒)は「判例上では、立件に違法性の認識の必要はない」と指摘しています。
確かに、違法駐車で切符を切られた後に、「ここが駐禁とは知らかった!」という理由で違反が無効になることはありません。立件されるされないのどちらであっても、アルバイトに参加した人が違法な犯罪に手を染めたという事実は残ります。
私は、政治活動は大切な暮らしの一部で、老若男女問わずもっと身近であってほしいと願っています。困っている当事者や支援者のひとり一人の声を署名という形で集めて、議会や行政に届けることは政治活動の大きな柱です。それを、こんな稚拙でだらしのない違法行為が行われニュースになれば、政治に詳しくなかったり興味がない人たちは、ただでさえ距離がある政治に対してより一層の嫌悪感をもつはずです。
それが悔しいです。
中日新聞社会面(1,31面)参考
» リコールってなに?
愛知県で行われたリコール運動の不正が話題となっています。
そもそもリコール運動とはなんでしょうか。
地方自治体では(愛知県とか名古屋市とかのことです)、知事や市長を直接投票で選ぶことができます。総理大臣は、国会議員だけで間接的に投票されるので、ここに違いがあります。
直接選べるので、逆に言うと直接辞めさせることもできるのです。その根拠となるのが、地方自治法第81条です。
知事や市長、議員は、民主主義という選挙で選ばれた人です。選挙で選ばれた人を辞めさせるには、同じく民主主義により「この人は(一度は当選したけども)やっぱり相応しくないからやめて欲しい」という署名を、有権者の総数のざっくり3分の1集めることができれば、リコール成立です(解職の請求ができます)。
つまり、リコール運動での署名を偽造するということは、選挙で投票用紙を偽造して他人の名前で勝手に投票をする感覚に近いです。違法かつ、民主主義の根幹、さらには政治や選挙そのものに対する信用性の悪化を招きます。
誰がどういった経緯で署名偽造が組織的に行われて、偽造バイトの資金はどう工面したのか、今後の調査で明らかになることを願いつつ、不正活動に対して抗議します。
そもそもリコール運動とはなんでしょうか。
地方自治体では(愛知県とか名古屋市とかのことです)、知事や市長を直接投票で選ぶことができます。総理大臣は、国会議員だけで間接的に投票されるので、ここに違いがあります。
直接選べるので、逆に言うと直接辞めさせることもできるのです。その根拠となるのが、地方自治法第81条です。
知事や市長、議員は、民主主義という選挙で選ばれた人です。選挙で選ばれた人を辞めさせるには、同じく民主主義により「この人は(一度は当選したけども)やっぱり相応しくないからやめて欲しい」という署名を、有権者の総数のざっくり3分の1集めることができれば、リコール成立です(解職の請求ができます)。
つまり、リコール運動での署名を偽造するということは、選挙で投票用紙を偽造して他人の名前で勝手に投票をする感覚に近いです。違法かつ、民主主義の根幹、さらには政治や選挙そのものに対する信用性の悪化を招きます。
誰がどういった経緯で署名偽造が組織的に行われて、偽造バイトの資金はどう工面したのか、今後の調査で明らかになることを願いつつ、不正活動に対して抗議します。
» 建築画ピーテル・サーンレダムとオルガン陳情
日経0205/36面
ピーテル・サーンレダムは日本ではあまり知られていませんが、教会堂の内部の建築画を好む画家です。
アムステルダム国立美術館が所有するサーンレダムの教会堂画(1636年油彩)には、遠近法の効いた教会堂奥に大きなオルガンが描かれています。このオルガンは、15世紀後半に設置されたものですが、プロテスタントに信仰が変わってからほとんど私用されなくなっていました。
その後1643年に、一部の演奏家や愛好家がオルガンを使用するように市議会に陳情しました。彼の絵は、まさにその陳情に関わる政治的な主張の手段として描かれたものでした。その甲斐もあってか、オルガンは修理され日常的に使用されるようになりましたとさ。
はて、キリスト教のプロテスタントはオルガンをあまり使用しないのでしょうか?
いずれにしても、何気ない美しい(しかも、来訪者もまばらな静けさのある教会堂画)がそんな政治的主張を秘めているなんて、その絵をみただけでは分かりません。こういう芸術の背景を楽しみ方法も、あるんですねぇ。
ピーテル・サーンレダムは日本ではあまり知られていませんが、教会堂の内部の建築画を好む画家です。
アムステルダム国立美術館が所有するサーンレダムの教会堂画(1636年油彩)には、遠近法の効いた教会堂奥に大きなオルガンが描かれています。このオルガンは、15世紀後半に設置されたものですが、プロテスタントに信仰が変わってからほとんど私用されなくなっていました。
その後1643年に、一部の演奏家や愛好家がオルガンを使用するように市議会に陳情しました。彼の絵は、まさにその陳情に関わる政治的な主張の手段として描かれたものでした。その甲斐もあってか、オルガンは修理され日常的に使用されるようになりましたとさ。
はて、キリスト教のプロテスタントはオルガンをあまり使用しないのでしょうか?
いずれにしても、何気ない美しい(しかも、来訪者もまばらな静けさのある教会堂画)がそんな政治的主張を秘めているなんて、その絵をみただけでは分かりません。こういう芸術の背景を楽しみ方法も、あるんですねぇ。
» 30歳代という年齢
30歳代という年齢
昨夜、年配の方に
「今年は(任期満了or解散総)選挙ですか、大変ですね。」
と投げかけられ、
「そうですね。大変ですが、頑張ります。」
と答えました。
人生はいくつになっても日々是好日(にちにちこれこうにち)で、常に新しい出会いや努力があります。
去年はウナギ釣りにハマったし、今年は第一子が誕生予定です。
一方で、「今までに何度か経験がある。」という事も少しずつ増えてきました。
20歳代は政治の道を選んだこともあり尚更、「やったこともないし、知識・知恵もない」という事が多く
失敗が多かったです。後悔はないけど、反省はたくさんあります。
30歳代はそうした過去の失敗や反省を活かして、「今度こそは」、という生き方ができる年代なのかもしれません。
昨夜、年配の方に
「今年は(任期満了or解散総)選挙ですか、大変ですね。」
と投げかけられ、
「そうですね。大変ですが、頑張ります。」
と答えました。
人生はいくつになっても日々是好日(にちにちこれこうにち)で、常に新しい出会いや努力があります。
去年はウナギ釣りにハマったし、今年は第一子が誕生予定です。
一方で、「今までに何度か経験がある。」という事も少しずつ増えてきました。
20歳代は政治の道を選んだこともあり尚更、「やったこともないし、知識・知恵もない」という事が多く
失敗が多かったです。後悔はないけど、反省はたくさんあります。
30歳代はそうした過去の失敗や反省を活かして、「今度こそは」、という生き方ができる年代なのかもしれません。
» Go To Eat キャンペーンについて
農林水産省が飲食店および農林漁業者を支援するためのキャンペーンですが、制度が複雑なので分かりやすく解説します。
大きく分けて、2種類の方法が選べます

①25%お得な、商品券を事前購入する
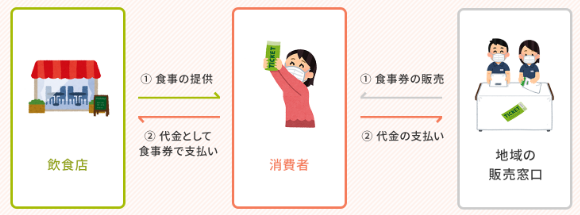
例えば、12,500円分の食事券を1万円で購入することができます。愛知県は、10月16日からファミリーマートで購入することができます。
詳細はこちら(愛知県公式)
https://gotoeat-aichi.jp/
②オンライン飲食予約でポイントを貰う
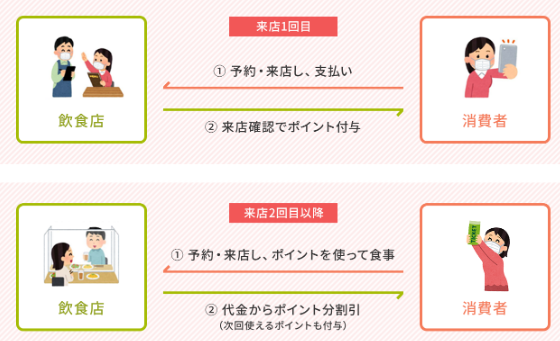
昼飯だと500円、夕食(15時~)だと1000円のポイントがもらえます。オンライン予約とは、飲食予約サイト(例えば食べログとか)経由で、期間中(ポイントが貰えるのは21年1月末まで開始時期は未定、ポイントが使えるのは3月末まで)に予約・来店すると次回以降に使えるポイントが貰えます。
よくある質問

オンライン飲食予約サイト運営については13社が認定されました。

その他、飲食店を経営されている方が、当キャンペーンに参加する方法はいくつか手段があり、またその参加方法は複雑です。興味のある方は個別にご連絡いただければ、簡単なご案内申し上げます。
当ページの画像等は農林水産省の公式ページから転載しました。詳細やより詳しいQ&Aなど、こちらをご覧ください。
https://gotoeat.maff.go.jp/
大きく分けて、2種類の方法が選べます

①25%お得な、商品券を事前購入する

例えば、12,500円分の食事券を1万円で購入することができます。愛知県は、10月16日からファミリーマートで購入することができます。
詳細はこちら(愛知県公式)
https://gotoeat-aichi.jp/
②オンライン飲食予約でポイントを貰う

昼飯だと500円、夕食(15時~)だと1000円のポイントがもらえます。オンライン予約とは、飲食予約サイト(例えば食べログとか)経由で、期間中(ポイントが貰えるのは21年1月末まで開始時期は未定、ポイントが使えるのは3月末まで)に予約・来店すると次回以降に使えるポイントが貰えます。
よくある質問

オンライン飲食予約サイト運営については13社が認定されました。

その他、飲食店を経営されている方が、当キャンペーンに参加する方法はいくつか手段があり、またその参加方法は複雑です。興味のある方は個別にご連絡いただければ、簡単なご案内申し上げます。
当ページの画像等は農林水産省の公式ページから転載しました。詳細やより詳しいQ&Aなど、こちらをご覧ください。
https://gotoeat.maff.go.jp/
» GDP速報値について【新聞各社読み比べ】
内閣府が17日に発表した4〜6月の国内総生産GDPの速報値は、前期比7.8%で年率換算で27.8%減となった。
各種新聞の抜粋です。詳細は、ぜひ各社新聞を購読ください。
日経新聞3面
感染再拡大に対する懸念が強く「V字回復」は難しい状況だ。民間エコノミストの間では、GDPが直前のピークである19年7〜9月期の水準を回復するのは24年頃との見方が多い。日経新聞が22人の民間エコノミストに今後の見通しを聞いた。7〜9月のGDPは内需・外需ともに反動増が期待される。ただ、予想通りの高成長でも4〜6月期の落ち込みの3分の1程度しか取り戻せず、水準は低いままにとどまる。予想では10〜12月期はさらに鈍化していく。実質GDPが500兆円を割るのは7年半ぶりで、12年末の第2次安倍政権発足前の水準まで逆戻りした。
中日新聞1面(関連は3、8、7面)
日本経済のV字回復は困難との見方が強く、年内に景気が2番底へと転落する恐れもある。
GDPの過半を占める個人消費は8.2%減で、消費税率を5%から8%に引き上げた際の4.8%減を大きく超える下げ幅だった。
毎日新聞1面(関連は3面)
7〜9月は反動でプラス成長に転じると民間シンクタンクは予想するが、再感染の広がりの影響で、回復のペースは鈍いとの見方が強まっている。個人消費の落ち込みは第1次オイルショックの6.0%を超え、戦後最悪の落ち込みだった。西村康稔担当相は「厳しい結果になった。ただし、各種支援策の効果もあり、年率マイナス30〜60%となったおう欧米各国と比べるば減少幅は抑えられた。」との見解を示した。
各種新聞の抜粋です。詳細は、ぜひ各社新聞を購読ください。
日経新聞3面
感染再拡大に対する懸念が強く「V字回復」は難しい状況だ。民間エコノミストの間では、GDPが直前のピークである19年7〜9月期の水準を回復するのは24年頃との見方が多い。日経新聞が22人の民間エコノミストに今後の見通しを聞いた。7〜9月のGDPは内需・外需ともに反動増が期待される。ただ、予想通りの高成長でも4〜6月期の落ち込みの3分の1程度しか取り戻せず、水準は低いままにとどまる。予想では10〜12月期はさらに鈍化していく。実質GDPが500兆円を割るのは7年半ぶりで、12年末の第2次安倍政権発足前の水準まで逆戻りした。
中日新聞1面(関連は3、8、7面)
日本経済のV字回復は困難との見方が強く、年内に景気が2番底へと転落する恐れもある。
GDPの過半を占める個人消費は8.2%減で、消費税率を5%から8%に引き上げた際の4.8%減を大きく超える下げ幅だった。
毎日新聞1面(関連は3面)
7〜9月は反動でプラス成長に転じると民間シンクタンクは予想するが、再感染の広がりの影響で、回復のペースは鈍いとの見方が強まっている。個人消費の落ち込みは第1次オイルショックの6.0%を超え、戦後最悪の落ち込みだった。西村康稔担当相は「厳しい結果になった。ただし、各種支援策の効果もあり、年率マイナス30〜60%となったおう欧米各国と比べるば減少幅は抑えられた。」との見解を示した。

最近のコメント